In het kort

De hoogteprofielen van de klimmen en klimmetjes meet ik met mijn fietscomputer, die behalve de afgelegde afstand ook de hoogte boven zeeniveau registreert. De hoogteprofielen worden vervolgens in stukjes langs de weg onderverdeeld. Deze hebben een lengte (dL) van 100 m voor heuvels in Nederland en 250 m voor klimmen in het buitenland. Voor elk stukje wordt uit begin- en eindhoogte het hellingspercentage (s) bepaald en daaruit de inspanning (dI):


met dI in kliminspanningspunten (kip), s in % en dL in meter. Het gaat hier om de inspanning voor zover deze groter is dan de inspanning op een horizontale weg. De zwaarte van de gehele klim wordt ten slotte berekend door de kliminspanningspunten langs de gehele afstand op te tellen. In woorden komt de methode erop neer dat het profiel in intervallen verdeeld wordt, dat de inspanning voor elk interval gelijk is aan het aantal hoogtemeters maal de steilte van de helling en dat vervolgens de inspanningen van alle intervallen bij elkaar opgeteld worden. Ten slotte wordt alles nog vermenigvuldigd met een constante (0.001), waardoor elke hoogtemeter bij een helling van 10% 1.0 kip oplevert. Een hoogtemeter levert slechts 0.5 kip op bij een helling van 5% en nog maar 0.1 kip bij een helling van 1%, etc. Hieronder wordt het een en ander in meer detail uitgelegd en bediscussieerd.

Opname van de profielen

De profielen neem ik op door de heuvels op te fietsen met mijn fietscomputer. Deze meet elke 5 seconden naast de afgelegde afstand ook de hoogte (boven zeeniveau). Een voorbeeld van een gemeten profiel staat in de figuur hierboven. Bij lagere snelheid is de dichtheid van de punten groter. Voorbeeld: bij een snelheid van 10 km/uur op een helling van 10% is er 1 meetpunt per 13.9 meter langs de weg en per 1.39 hoogtemeters, terwijl men bij een snelheid van 20 km/uur op een helling van 5% 1 meetpunt per 27.8 meter langs de weg en 2.78 hoogtemeters krijgt. Omdat de hoogtebepaling door de fietscomputer via meting van de luchtdruk gebeurt, worden de hoogteprofielen 'geijkt'. Dit doe ik door het gemeten profiel omhoog- of omlaag te schuiven zodanig dat de hoogte van het hoogste punt (eindpunt) van de klim overeenkomt met de hoogte bepaald op de website van AHN (Actuele Hoogtebestand Nederland). De files met de meetpunten zet ik op mijn computer, waar ze met een zelfgeschreven computerprogramma verwerkt worden. Het programma bepaalt voor elk '100 meter punt' langs de helling de hoogte door lineair te interpoleren tussen de meetpunten (zie figuur hierboven).

Kliminspanningspunten (kip)

De zwaarte van de klimmen wordt beoordeeld door het aantal Kliminspanningspunten (kip) te berekenen. Deze index is een vereenvoudigde versie van de bekende Cotacol-index. Kliminspanningspunten worden berekend (zie ook de figuur hierboven) door het hoogteprofiel van de heuvel in te delen in stukjes van 100 meter (langs de weg) en vervolgens voor elk stukje van 100 meter:

• het aantal hoogtemeters te bepalen
• de hoogtemeters om te zetten in het hellingspercentage (10 hoogtemeters komen overeen met een hellingspercentage van 10%)
• de hoogtemeters volgens de vergelijking boven aan deze pagina om te zetten in het aantal kliminspanningspunten

Ten slotte worden de kliminspanningspunten langs het hele traject bij elkaar opgeteld.

De methode ontleent zijn kracht aan twee aspecten. Ten eerste houdt de methode, door opdeling in stukjes van 100 meter en door optelling langs de hele helling, rekening met alle variaties in zwaarte langs die helling (behalve variaties binnen stukjes van 100 meter). Ten tweede stijgt het aantal kliminspanningspunten kwadratisch met de helling, dat wil zeggen dat het aantal punten vier keer zo groot wordt als het hellingspercentage verdubbelt, bij eenzelfde afgelegde afstand. En dat betekent weer dat eenzelfde aantal hoogtemeters het dubbele aantal kliminspanningspunten oplevert als het hellingspercentage verdubbelt.

Waarom deze Zwaarte-index?

Veel andere methodes, die gebruikt worden om de zwaarte van fietsbare heuvels te beoordelen, gebruiken wat ik 'bulkgetallen' noem. Bulkgetallen beschrijven eigenschappen van de heuvel met een enkel getal. Voorbeelden zijn een beschrijving van de hoogte met het totale aantal hoogtemeters en van de hellingshoek met het (over de gehele lengte van de klim) gemiddelde hellingspercentage. Het totale aantal hoogtemeters is de meest eenvoudige maat voor de zwaarte van een heuvel, maar te grof. Een bepaald aantal hoogtemeters overbruggen is immers zwaarder naarmate de helling steiler is. Om daar rekening mee te houden heeft het tijdschrift Fiets voorgesteld om de zwaarte te bepalen door het product van het totale aantal hoogtemeters en het gemiddelde hellingspercentage te nemen.

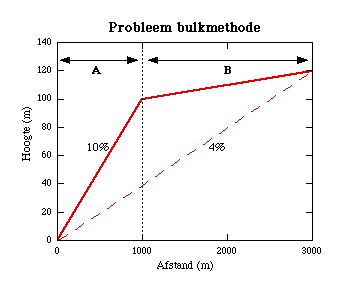
Welnu, dat kan goed mislopen. Neem als voorbeeld de denkbeeldige heuvel in de figuur hierboven (Probleem bulkmethode; de dikke rode lijn). Het gedeelte A overbrugt 100 hoogtemeters over een afstand van 1000 meter. Het heeft dus een hellingspercentage van 10% en zou een Fiets-zwaarteindex van 1000 (100*10) krijgen. De gehele heuvel (A en B) overbrugt 120 hoogtemeters over een afstand van 3000 meter. Dat is een gemiddeld hellingspercentage van 4%. Daaruit volgt een Fiets-zwaarteindex van 480 (120*4). De gehele heuvel wordt dus als minder dan half zo zwaar beoordeeld als het gedeelte A alleen, terwijl het geheel het gedeelte A omvat en dus zeker zwaarder zou moeten zijn dan het gedeelte A! Ik concludeer dat gebruik van het gemiddelde hellingspercentage in een zwaarteindex voor heuvels opfietsen niet deugt.

Veel beter is het om de klim in kleine stukjes op te delen, per stukje de zwaarte te bepalen en ten slotte de zwaartes langs de hele helling op te tellen. Op die manier wordt er rekening gehouden met alle variaties in de zwaarte langs die helling.

Deze aanpak vindt men terug in de Cotacolmethode, die o.a. gebruikt is in het boekwerk over fietsbare hellingen in België (Encyclopedie Cotacol). Ook de vergelijking, die het verband tussen hellingspercentage en inspanning beschrijft, heb ik van de Cotacolmethode overgenomen.

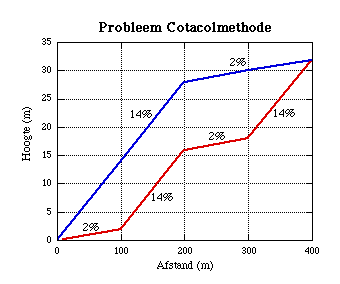
De volledige Cotacol-methode kent echter een term, die corrigeert voor variaties in hellingspercentage. Deze heb ik weggelaten. Aan de hand van de figuur hierboven (Probleem Cotacolmethode) zal ik uitleggen waarom ik dat gedaan heb. Zonder correctieterm zouden de denkbeeldige hellingen in de figuur beide beoordeeld worden met een zwaarte van 49.2 Cotacolpunten. De variaties in hellingspercentage leveren echter voor de rode helling een correctieterm van 1.75 op, waarmee het aantal Cotacolpunten vermenigvuldigd dient te worden (de zwaarte wordt dan 86.1 Cotacolpunten). De blauwe helling verdient volgens de Cotacolmethode geen correctie en blijft op 49.2 punten steken. Dat lijkt me niet juist. Sommige fietsers zullen van mening zijn dat de rode helling zwaarder is, omdat ze het ritme vaker moeten aanpassen. Anderen zullen de blauwe helling juist zwaarder vinden, omdat er op de rode helling een stuk is om even te herstellen. Velen zullen echter twijfelen, omdat ze het gevoel hebben dat de inspanningen, die nodig zijn om de beide hellingen op te fietsen, ongeveer gelijk zijn. Mijn conclusie is dat een correctieterm voor variaties in hellingspercentage beter helemaal weg kan worden gelaten en dat, als hij dan toch meegenomen moet worden, voor elk soort helling dicht in de buurt van de 1 zou moeten liggen. Die factor van 1.75 voor de rode helling in de figuur is zeker niet gerechtvaardigd.

Op basis van al deze overwegingen heb ik de door mij ingemeten hellingen beoordeeld met de Cotacolmethode met weglating van de correctieterm voor variaties in hellingspercentage.

Fouten

Twee foutenbronnen beïnvloeden de berekening van de zwaarte van de heuvels, namelijk de vorm (kwadratisch) van de vergelijking, waarmee het hellingspercentage omgezet wordt in inspanning, en de meting van de profielen.

Terwijl ik denk dat mijn aanpak om de zwaarte van een helling te beoordelen (profiel meten, in kleine stukjes verdelen, hellingspercentages bepalen en omzetten in inspanning, optellen over alle kleine stukjes) juist is, is de gebruikte vergelijking vermoedelijk niet correct. Deze is, voor zover mij bekend, gebaseerd op gevoel of theorie en niet op metingen. Echter, alleen "meten is weten". Hoogstwaarschijnlijk zal een op metingen gebaseerde vergelijking niet kwadratisch zijn, zoals de door mij gebruikte vergelijking. Meten kan door tegelijk hellingspercentage en inspanning te meten bij racefietsers. Het is nuttig om er even bij stil te staan dat de inspanning op een gegeven helling afhangt van wie er op de fiets zit, van het verzet en van hoe men de helling opfietst. Het scheelt flink in inspanning of men even flink de helling opknalt of meer behoudend omhoogfietst. Er zal dus bij een gegeven hellingspercentage veel spreiding in de inspanning optreden. Een op metingen gebaseerde vergelijking zal dan ook het gemiddelde over een groot aantal metingen beschrijven. Lijkt me een interessant onderwerp van onderzoek voor bewegingswetenschappers!

In de gemeten profielen kunnen op vier manieren fouten sluipen:

1. In de afstandsmeting
   Om te onderzoeken hoe groot de fout in de afstandsmeting is, heb ik drie keer een afstand van ongeveer 10 km langs verschillende wegen met mijn fietscomputer opgemeten en vergeleken met de langs de weg staande hectometerpaaltjes. Steeds was de fout niet groter dan 1%. Deze fout is dus verwaarloosbaar.


2. Een systematische fout in de hoogteverschillen (een systematische fout is een fout, waarvan het gemiddelde over vele metingen niet gelijk aan nul is).
   Deze fout zou ik kunnen bepalen door een nauwkeurig bekend hoogteverschil meerdere keren op te meten. Dat heb ik echter nog niet gedaan. Zo'n experiment is in Midden-Nederland niet goed uitvoerbaar door de kleine hoogteverschillen en onzekerheid in de hoogte of ligging van begin- en eindpunt van zo'n meting.


3. Ruis in de hoogtemetingen (ruis wordt gevormd door afwijkingen, waarvan het gemiddelde over vele metingen gelijk aan nul is).
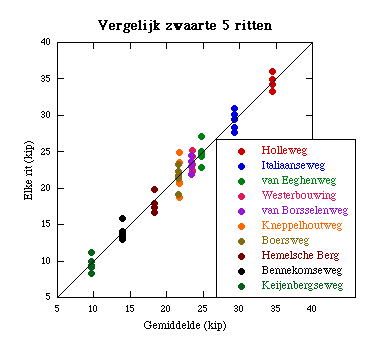
   Dit is inderdaad het geval. Als je stilstaat, geeft de fietscomputer niet steeds dezelfde hoogte aan, maar flippert wat heen en weer. Ook blijkt dit uit de vergelijking van vijf profielmetingen langs de Westerbouwing, zie de eerste figuur hieronder (Vergelijk ritten Westerbouwing). De vraag in vervolgens hoe groot de invloed van die ruis op de zwaarte is. Om dat te onderzoeken heb ik de profielen van tien hellingen ieder vijf keer opgemeten en steeds de zwaarte bepaald. Het resultaat is zichtbaar in de tweede figuur hieronder (Vergelijk zwaarte 5 ritten), waarin op de horizontale as de gemiddeldes over de vijf ritten staan en op de vertikale as de waardes van de ritten afzonderlijk. De fout blijkt niet verwaarloosbaar te zijn en is, sorry voor de wiskunde, gelijk aan 1.4 kip (dat wil zeggen dat een willekeurige meting een kans heeft van 67% om minder dan 1.4 kip af te wijken van de werkelijke waarde).


4. Traagheid van de hoogtemeter
   De hoogtemeter zou niet instantaan kunnen reageren als de hoogte verandert, maar wat achter kunnen lopen op de werkelijke veranderingen in hoogte. Ik heb dit onderzocht door het profiel van de Westerbouwing op te meten met zeer geringe snelheid (omhoogwandelen met de fiets aan de hand). Dit profiel wijkt hoogstens subtiel af van de vijf profielen, die gemeten zijn met mijn normale fietssnelheid (zie de figuur Vergelijk ritten Westerbouwing). Desondanks is de uit dit "langzame profiel" bepaalde zwaarte groter dan de zwaartes bepaald uit de andere vijf profielen. Enige traagheid van de hoogtesensor is vrijwel zeker toch aanwezig en beïnvloedt de bepaling van de zwaarte. Om een degelijke conclusie te trekken, dient de langzame klim vaker gemaakt te worden.

Samengevat, denk ik dat onjuistheid van de vergelijking, die hellingspercentage omzet in inspanning, de grootste foutenbron is. Ruis in de hoogtemetingen komt op de tweede plaats. De invloeden van een systematische fout in de hoogtemetingen en van traagheid van de hoogtemeter zullen vermoedelijk gering zijn, maar moeten nog nader bekeken worden.

Discussie

Ten slotte wil ik nog twee opmerkingen maken. Ik hoor vaak opmerkingen als "hoe kan Camerig de zwaarste heuvel van Nederland zijn; de Keutenberg vind ik veel zwaarder". Mensen, die dergelijk opmerkingen maken, gaan op hun gevoel over het zwaarste moment van een klim af. Ze vinden een klim zwaarder naarmate ze dichter bij afstappen komen Inderdaad noopt de Keutenberg, omdat hij steiler is, racefietsers eerder tot afstappen dan de Camerig. Ik heb echter als maat voor de zwaarte geprobeerd de totale inspanning (voor zover deze groter is dan de inspanning op een horizontale weg) te schatten. Daarbij telt niet alleen de steilte, maar ook de totale duur van de inspanning en die is veel groter bij de Camerig (183 hoogtemeters) dan bij de Keutenberg (83 hoogtemeters). Vandaar die eerste plaats voor de Camerig.

Vaak is het bepalen van het begin- en het eindpunt van de heuvels gemakkelijk. Iedereen zal het erover eens zijn waar de Eyserbosweg begint, namelijk waar deze weg begint in het dorpje Eys. Het hellingspercentage is meteen aanzienlijk (9% voor de eerste 100 meter). Het komt echter ook vaak voor dat de keuze van het begin- en het eindpunt van een heuvel lastig is. Dat is het geval als het begin of het einde heel licht oploopt. De vraag is dan steeds of dit stuk meegenomen moet worden of niet. Een goed voorbeeld is de Posbank (Veluwezoom). Deze eindigt bij mij met het steile stuk over de Schietbergseweg naar de Posbank en eindigt daarmee op 82 meter hoogte. Men kan daarna echter ook nog 1200 meter doorrijden naar de Tafelberg (gemiddeld hellingspercentage: 1.3%). Ik heb de subjectieve keus gemaakt om dit stuk niet mee te nemen. Wat ik kwijt wil is dat het wel of niet meenemen van dit stuk weinig invloed heeft op de berekende zwaarte, (er zouden 3 kip bijkomen; nu zijn het 36 kip) omdat het hellingspercentage zo klein is. Gelukkig is dit verband steeds aanwezig: als een eventueel begin- of eindstuk van een heuvel licht helt, is er vaak twijfel over het wel of niet meenemen van dit stuk, maar de invloed op de zwaarte is gering.